Salgótarján várható hőmérséklet előrejelzése a egyik legfontosabb része az időjárás előrejelzéseknek. Az előrejelzések megbízhatósága rendkívül összetett kérdés, a rendelkezésünkre álló rengeteg adat, fejlett műszerek, kifinomult algoritmusok és hatalmas számítási képességgel rendelkező szuperszámítógépek ellenére is elmondható, hogy míg a másnapi várható időjárást 90-95%-os pontossággal meg tudjuk mondani, addig 4 napra előre 75-90%, a heti előrejelzés 65-80%-os pontossággal, 10 nappal előre pedig már csak 60% körüli valószínűséggel jósoltható meg a várható időjárás.
Az előrejelzések elkészítésében sűrű mérőhálózatok segítik a meteorológusok munkáját – ahhoz, hogy pontos előrejelzések készülhessenek a légkör több pontjáról be kell szerezni a méréseket. Így ma már nem csak földfelszínen kialakított állomások vannak, a légkör bizonyos magassági szintjein is végeznek méréseket úgynevezett meteorológiai ballonok (főleg nagyobb városokban bocsátanak fel naponta ilyeneket) segítségével. Ha megvannak az adatok, képbe kerülhetnek a számítógépes modellek, amelyek segítségével bizonyos képletek és számítások után térképre lehet vetni az adatokat. Ez ma már automatizmus, az ember már csak a térképek, diagramok értelmezéséhez kell.
Minél több adatot táplálnak a szimulációkat lefuttató szuperszámítógépekbe a Földet körülölelő háromdimenziós légkörről, annál pontosabb a differenciálegyenletek megoldása. A glóbuszon elhelyezett több százezer egyedi mérőállomás soknak tűnhet, pedig az egyenletek tökéletes megoldásához közel sem elég. Nem szólva arról, hogy a Föld nehezen hozzáférhető pontjain, például a sivatagokban, óceánok, tengerek közepén, szakadékokban, a sarkvidékeken alig-alig akadnak szenzorok. Ugyancsak kevés adat származik a légkör magasabban található részeiről, épp onnan, ahol az időjárási jelenségek zajlanak.
Magyarországon a földfelszín közelében 250, a légkört 10 percenként szondázó automata mérőállomás működik. Magaslégköri eseményeket figyelő, úgynevezett troposzféra-állomás viszont csak Szegeden és Budapesten van, és az itt található műszerekkel is csak egy mérést végeznek minden 12 órában.
Az adatok hiányosságán valamelyest enyhít, hogy a légkört felülről is szondázza több mint ezer meteorológiai műhold. A számítógépes szimulációkban kulcsszerepet játszó hidro-termodinamikai egyenleteknek azonban így is legfeljebb csak közelítő megoldása lehet. Az sem mindegy, milyen adat számunkra a legfontosabb, ugyanis miközben a várható hőmérséklet egész precízen kiszámítható, a csapadékmennyiség és a szélerősség előrejelzése rendszerint lényegesen pontatlanabb.
A magyarországi időjárás előrejelzését megnehezíti, hogy hazánk három nagy éghajlati zóna határán fekszik. Így az időjárási folyamatokat kontinentális vagy óceáni, máskor mediterrán hatások, esetenként ezek együttese határozza meg. Nehezíti az előrejelzést az is, hogy hazánk egy viszonylag zárt medencében fekszik, és a környező hegységeknek az időjárási mozgásrendszerekre gyakorolt hatásai gyakran nehezen kiszámíthatók. A sikeres hazai előrejelzéshez szükség van a szinte egész Európában, s az Atlanti-óceán nagy részén uralkodó időjárás ismeretére. Az itt lezajló nagyléptékű légköri folyamatok alakítják ugyanis a Kárpát-medence időjárását is.
A várható időjárás kiszámításához különböző modelleket alkalmazunk, ezek közül a legismertebbek:
A numerikus időjárás-előrejelzés
Valós időjárási adatokat alapul véve matematikai modelleket alkalmaz lokális vagy globális időjárási viszonyok előrejelzésére. Bár az első lépéseket az 1920-as években tették, a numerikus időjárás-előrejelzés csak a számítógépek elterjedése után vált lehetségessé. A nagy kiindulási adatbázisok és az időjárás előrejelzéséhez szükséges komplex számításokhoz, amennyiben azt olyan részletességgel kívánják elvégezni, hogy az eredmény hasznos legyen, napjaink legnagyobb teljesítményű szuperszámítógépeire van szükség. A numerikus modellek azt veszik alapul, hogy a légkör folyadék módjára viselkedik. A numerikus időjárás-előrejelzés modelljeiben a légkör egy adott állapotára vonatkozó adatokat táplálják a légkör viselkedését leíró termodinamikai és folyadékdinamikai egyenletekbe, amelyek segítségével a folyadék jövőbeni helyzetét lehet meghatározni.
A légkör pillanatnyi és előrejelzett állapotát fizikai törvények matematikai formába öntött egyenleteivel, az ún. hidro-termodinamikai egyenletrendszerrel adjuk meg. Ennek a prognosztikus egyenletrendszernek a segítségével, amennyiben ismerjük az időjárási elemek adott időpontban felvett értékeit, meghatározható azok jövőbeli értéke. A meghatározandó állapothatározók a szélsebesség komponensei, a hőmérséklet, a nedvesség és a légnyomás.
Az egyenletrendszer első egyenlete Newton második törvénye, mely azt írja le, hogy egy test mozgását a rá ható erők eredője határozza meg. A mozgásegyenlet három egyenletből áll, hiszen a légköri mozgások háromdimenziósak. Így ezeket felbonthatjuk x, y és z irányú komponensekre. A mozgásrendszerek leírásánál az x irány Kelet, az y Észak, a z pedig a zenit (a sík felszínre merőleges, függőleges irány) felé mutat. Az egyes irányokba eső komponensek eredője határozza meg végül a tényleges szélirányt. Az energia megmaradását az ún. termodinamikai egyenlet, a tömegmegmaradást pedig a kontinuitási egyenlet fejezi ki. Az egyenletrendszert az ideális gáz egyenlete teszi teljessé.
A fenti hat egyenlet az időjárás-előrejelzés alapja. Ezeket az egyenleteket kell megoldani minden egyes rácspontra az egész légkörre (GCM – General Circulation Model), vagy annak egy tartományára (LAM – Limited Area Model). A rácspontok számát a rácstávolság és a vertikális szintek száma határozza meg. A szintek általában sűrűbben helyezkednek el a légkör alsó tartományában, ahol az időjárási folyamatok jelentős része végbemegy. A horizontális felbontás a modellekben általában néhány 10 km-től néhány 100 km-ig terjed, a szintek száma pedig néhányszor 10.
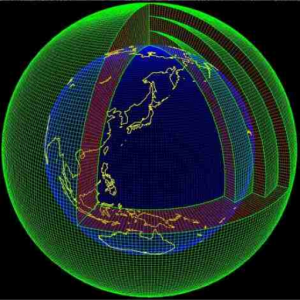 A probléma nagyságát illusztrálandó tekintsük a következő példát: Egy 60 km-es horizontális felbontású modell esetén a teljes földfelszínt több mint 134 000 rácspont határoz meg. Mindez 31 szintre számolva már kb. 4 millió rácspontot tesz ki, mely a hat egyenlet alkalmazásával 24 millió ismeretlent és 24 millió egyenletet jelent. Ezt megoldva megkapjuk az eredményt a következő időlépcsőre, ami általában 4 perc. Ha hosszabb időlépcsőt választanánk, gyorsan növekvő hibák (ún. nemlineáris instabilitások) lépnének fel az előrejelzésben, s az eredmény már egy napra is használhatatlan lenne. Így egynapi előrejelzéshez a 24 millió egyenletet 4 perces időlépcső alkalmazásával 360-szor kell megoldani.
A probléma nagyságát illusztrálandó tekintsük a következő példát: Egy 60 km-es horizontális felbontású modell esetén a teljes földfelszínt több mint 134 000 rácspont határoz meg. Mindez 31 szintre számolva már kb. 4 millió rácspontot tesz ki, mely a hat egyenlet alkalmazásával 24 millió ismeretlent és 24 millió egyenletet jelent. Ezt megoldva megkapjuk az eredményt a következő időlépcsőre, ami általában 4 perc. Ha hosszabb időlépcsőt választanánk, gyorsan növekvő hibák (ún. nemlineáris instabilitások) lépnének fel az előrejelzésben, s az eredmény már egy napra is használhatatlan lenne. Így egynapi előrejelzéshez a 24 millió egyenletet 4 perces időlépcső alkalmazásával 360-szor kell megoldani.
Ezt a nagymennyiségű számítást csak igen gyors szuperszámítógépek segítségével lehet elvégezni a rendelkezésre álló idő alatt. Ahhoz, hogy az előrejelzés időben elkészüljön, jóval gyorsabban kell számolni, mint ahogy a valós időjárási folyamatok alakulnak.
Ensemble előrejelzés
1963-ban Edward Lorenz felvetette, hogy nem lehetséges az időjárás pontos előrejelzése, mivel a légkör viselkedését leíró folyadékdinamikai elméletek kaotikus természetűek, kutatásaival egyben lefektetve a káoszelmélet alapjait is. Ezen felül az időjárási megfigyelőállomások nem egyenletesen fedik le a Föld felszínét, ezért a rendelkezésre álló adatok térben és időben is korlátozottak – pl. relatíve kevés információ áll rendelkezésre a Csendes-óceán állapotáról, ami bizonytalanságot eredményez a légkör kiindulási állapotának meghatározásánál. Az ensemble előrejelzések két nagy változata a multi-modell ensemble, amely a modellek felírása során fellépő bizonytalansági tényezőket több modell együttes használatával kompenzálja. A multi-modell módszer az egyik legegyszerűbb ensemble előrejelzés, egyik példája az európai SRNWP-PEPS operatív multi-modell ensemble, amelyben 21 európai ország 24 modellel vesz részt.
A másik lehetséges eljárás a multi-analízis ensemble, amely különböző kezdeti feltételekkel vagy technikákkal készített előrejelzéseket használ. A két fenti eljárást együttesen is használják, a multi-modell multi-analízis ensemble pl. a spanyol meteorológiai szolgálat SREPS módszere.
Az ensemble-előrejelzések egyik problémája az eredmények megjelenítése. Kis elemszámú ensemble elemzéseknél az egyes tagokat külön-külön jelenítik meg, de nagy elemszámú ensemble rendszer esetén ez már nem áttekinthető. Ilyenkor használják az ún. ensemble átlagot, illetve mediánt a különböző előrejelzések egyesítésére.
A hőmérők típusai
 A meteorológiai gyakorlatban a hőmérőket a mérés elve alapján az alábbi osztályokba sorolhatjuk: 1. a térfogatváltozáson alapuló hőmérők 2. ellenállás-hőmérők 3. infrahőmérők.
A meteorológiai gyakorlatban a hőmérőket a mérés elve alapján az alábbi osztályokba sorolhatjuk: 1. a térfogatváltozáson alapuló hőmérők 2. ellenállás-hőmérők 3. infrahőmérők.
A hagyományos, analóg hőmérők rendre a testek térfogatváltozásán alapulnak. Ide tartoznak a folyadék- és fémhőmérők. Előbbiek az aktuális hőmérséklet mérésére használt műszereknél elterjedtek (termométerek), míg utóbbiak leginkább a hőmérsékletíró műszereknél (termográfok) használatosak. A fémhőmérők pontossága elmarad a folyadékhőmérőkétől, azonban az elektromos hőmérők rendszeresítését megelőzően csak így volt lehetőség a hőmérséklet folyamatos rögzítésére.
Folyadékhőmérők
A hőmérséklet-változás hatására a folyadékok térfogata megváltozik. A folyadékhőmérők egy nagy térfogatú tartályból és egy hozzá tartozó, kis térfogatú csőből (kapillárisból) állnak. A tartályban lévő anyag kiterjedésének megváltozása – hőváltozás esetén – csak a csőben tud lejátszódni. Elméletileg bármilyen folyadék alkalmas lehet 3 hőmérő készítésére, azonban figyelemmel kell lenni az anyag fagyás- és forráspontjára, hőtágulási együtthatójára és párolgására.
A legtöbb meteorológiai állomáson többféle folyadékhőmérőt is használnak illetve használtak. Mivel azonban az automata és hagyományos mérések között hosszabb távon sem volt kimutatható jelentős eltérés, így a 2010-es évek közepétől a legtöbb helyen a hagyományos hőmérőkkle mért adatok már nem kerülenk rögzítésre.
Az állomási hőmérő nagy pontosságú, Celsius-skálájú, higannyal töltött hőmérő. Mérési tartománya Közép-Európában –35 °C-tól +45 °C-ig terjed. Skálája 0,2 °C-os beosztású, a leolvasás azonban 0,1 °C-os pontossággal történik. A leolvasáskor „szemünk mindig egy magasságban legyen a hőmérő higanyszálának végével, tekintetünk merőlegesen essék a számlapra, hogy ezáltal az ún. parallaxis hibát elkerüljük”. Az állomási hőmérőt korábban óránként, majd az automata műszerek rendszeresítését követően csak kontroll jelleggel, a szinoptikus főterminusokkor (0, 6, 12, 18 UTC) kellett leolvasni a főállomásokon.
A Fuess-féle maximumhőmérő Hasonló szerkezetű, mint az állomási hőmérő, működési elve azonban hasonlít egy lázmérőére. A tartály aljára vékony üvegpálca van forrasztva, ami benyúlik a kapillárisba, ezzel növelve a higany súrlódását. A hőmérséklet emelkedésekor a higany átpréselődik az akadályokon, de hűléskor már nem tud visszafolyni a tartályba, a szűkületben a higanyszál megszakad, a kapillárisban marad és megőrzi a maximális hőmérsékletkor felvett állapotát. Annak érdekében, hogy a higanyszál melegedéskor ne csússzon magasabbra, a vízszinteshez képest 2°-kal megdöntve kell elhelyezni úgy, hogy a higanygömb felőli rész legyen alacsonyabban. Függőleges helyzetben kell leolvasni, majd lerázni. Skálája 0,5 °C-os beosztású, a leolvasás tized pontossággal történik, becsléssel. Naponta kétszer, a 6 és 18 UTC-s főterminusokkor kell leolvasni. A mért adat az elmúlt 12 órára vonatkozik. A napi maximum-hőmérséklet tehát a 6 és 18 UTC között mért legmagasabb hőmérséklet.
A maximum-hőmérséklet mérése történhet a Six-rendszerű maximum–minimum hőmérővel is. A műszer előnye, hogy a maximum-, a minimum- és az aktuális hőmérséklet is egyetlen hőmérővel mérhető. Egy U alakú csőbe alkoholt, higanyt és gázt töltenek, a mérőfolyadék szerepét az alkohol tölti be. Leolvasáskor a hőmérő egy mágnessel vagy egy gomb megnyomásával alaphelyzetbe állítható. A műszer a Fuess-féle maximumhőmérőhöz képest pontatlannak számít, így meteorológiai alkalmazása kevésbé elterjedt. A meteorológiai állomásokon használatos még a Fuess-féle minimumhőmérő. A higany fagyáspontja (–39 °C) miatt a hőmérőbe színezett alkoholvegyületet vagy toluolt töltenek, hogy a –39 °C-nál alacsonyabb hőmérsékletek mérése is lehetségessé váljon. A csőben egy üvegpálcika van elhelyezve. A folyadékszál hőmérséklet-csökkenéskor magával húzza a pálcikát, a hőmérséklet emelkedésekor viszont körülfolyja, és változatlan helyen hagyja, így megállapítható a mérési időszak alatt felvett minimum-hőmérséklet. A műszert naponta kétszer, 6 és 18 UTC-kor kell leolvasni. A radiációs (fűszinti) minimum-hőmérséklet mérésére szintén a Fuess-féle minimumhőmérő használatos, amelyet a talajtól 5 cm-es magasságban helyeznek el. A műszert 6 UTC-kor kell leolvasni. A talajhőmérséklet mérése higannyal töltött, kampós végű, felszíni talajhőmérőkkel történik 2, 5, 10 és 20 cm mélységben. A mélységi talajhőmérők 50 és 100 cm mélyen vannak elhelyezve. Előbbieket naponta négyszer, főterminuskor, utóbbiakat csak 12 UTC-kor kell leolvasni. 2.1.2. Elektromos hőmérők A hőmérséklet-változás következtében megváltoznak az anyagok (fémek) elektromos tulajdonságai is. Ezen a tényen alapul az elektromos hőmérők működése.
Ellenállás-hőmérők
 A tiszta fémek elektromos ellenállása a vezető hőmérsékletével megváltozik, jó közelítéssel egyenesen arányosan. Leginkább platina, nikkel, volfrám illetve ötvözetlen réz alkalmas ellenállás-hőmérő készítésére. A meteorológiai gyakorlatban az ún. Pt100-as platinahőmérő az elterjedt, amelynek 0 °C-on pontosan 100 Ω az ellenállása. A szenzor pontossága – magyarországi körülmények között – 0,3 °C-on belül marad.
A tiszta fémek elektromos ellenállása a vezető hőmérsékletével megváltozik, jó közelítéssel egyenesen arányosan. Leginkább platina, nikkel, volfrám illetve ötvözetlen réz alkalmas ellenállás-hőmérő készítésére. A meteorológiai gyakorlatban az ún. Pt100-as platinahőmérő az elterjedt, amelynek 0 °C-on pontosan 100 Ω az ellenállása. A szenzor pontossága – magyarországi körülmények között – 0,3 °C-on belül marad.
A termisztorok Hasonlóan az ellenállás-hőmérőkhöz, itt is az ellenállás megváltozását vesszük a mérés alapjául, ellenben a félvezetőknél a hőmérséklet-változás és az ellenállás között nem lineáris, hanem exponenciális összefüggés áll fenn. A termisztorok többségénél az ellenállás a hőmérséklet növelésével csökken. Előnyük, hogy gyorsan reagálnak a hőmérséklet változásaira és alacsony hőmérsékleten nagy pontosság érhető el velük (a nagyobb ellenállás-különbségek miatt), hátrány viszont, hogy nem lineáris a kapcsolat a hőmérséklet és az ellenállás között. Magasabb hőmérsékleteknél a pontosságuk lényegesen elmarad az ellenállás-hőmérőkhöz képest.
A hőmérők elhelyezése a meteorológiai állomásokon A szinoptikus meteorológiai állomásokon fontos, hogy olyan méréseket végezzünk, ahol nem, vagy csak kevésbé érvényesülnek lokális hatások. A mérőhálózat sűrűsége és a numerikus modellek bemenő adataival szemben támasztott elvárásaink is azt kívánják meg, hogy a mért adat ne csak az állomásra, hanem annak viszonylag nagyobb környezetére is reprezentatív legyen. Erre a célra az olyan területek felelnek meg, amelyek minden irányból nyitottak és a mérést nem zavarja közeli épület, növényzet vagy egyéb tereptárgy. A hőmérséklet mérését a nemzetközi előírásoknak megfelelően 1,2 és 2 méter között kell elvégezni. Magyarországon a léghőmérséklet mérése pontosan 2 méteres magasságban történik. A hőmérséklet mérésekor alapvető fontosságú, hogy a hőmérő – legyen akár folyadékhőmérő, akár elektromos szenzor – a mérendő közeg, esetünkben a levegő tényleges hőmérsékletét mérje, és csak azzal álljon kölcsönhatásban. A hőmérőt emiatt védeni kell: – a rövidhullámú sugárzástól, – a csapadéktól, – a széltől. A hőmérők elhelyezésére a XIX. század végén a Brit Meteorológiai Társaság (Royal Meteorological Society) a Stevenson-féle hőmérőházat javasolta. Magyarországon ez csak a XX. század első felében vált elterjedtté. A hőmérőház fából készült, kívül-belül fehérre festett, kettős zsaluzású. Véd a közvetlen napsugárzástól, és az erős szél hatását is gyengíti, miközben a zsaluzás biztosítja a légmozgást, a hőmérőház szellőzését. Ajtaja mindig északi irányba nyílik. A ház mérete kellően nagy ahhoz, hogy a száraz-nedves hőmérőpár (pszichrométer), a szélsőértékhőmérők és a leolvasáshoz szükséges egyéb kellékek (pl. aspirátor) is elférjenek benne. Az elmúlt évtizedekben a meteorológiai szolgálatnál folyamatosan átálltak az automata, elektromos mérésekre. A kis méretű szenzorok már a legtöbb esetben tányéros árnyékolóban kerülnek elhelyezésre. A méretből adódóan a hőmérő szellőzése jobban megoldott, mint a Stevenson-féle házban, így a hőmérséklet-változásokat is gyorsabban érzékeli a műszer.
Infra hőmérők
A non-kontakt infravörös hımérsékletmérés elınye a gyorsaság, az extrém körülmények közötti biztonságos mérés, az interferencia hiánya és az a képesség, hogy magas hımérsékleten (egészen 3000ºC-ig) is lehet hımérsékletet mérni. Figyelembe kell venni, hogy csak felületek hımérsékletét lehet megmérni!
Minden anyag bocsát ki infravörös sugárzást, amennyiben a hımérséklete abszolút 0 fok (-273°C) felett van, és a sugárzás mértéke függ a test hımérsékletétıl. Ezt nevezzük jellemzı vagy karakterisztikus sugárzásnak, melynek az oka a molekulák anyagon belüli mozgása. Ennek a mozgásnak az intenzitása az objektum hımérsékletétıl függ. Mivel a molekuláris mozgás töltéssel rendelkezı részecskék elmozdulásával jár, a test elektromágneses sugárzást (foton részecskéket) bocsát ki. Ezek a fotonok a fény sebességével mozognak és a fénytan alapelveinek megfelelıen viselkednek. El lehet ıket téríteni, fókuszálni lehet ıket lencsével, vagy vissza lehet ıket verni egy visszaverı felületrıl. Ennek a sugárzásnak a spektruma 0,7-tıl 1000 µm hullámhosszig terjed, ebbıl kifolyólag saját szemünkkel nem érzékeljük. Ez a spektrális tartomány a látható fénytartományon belül a vörös tartományába esik, ezért a latin eredető elıtaggal infravörös fénynek nevezik
Mik az elınyei a non-kontakt hımérsékletmérésnek? Gyors mintavétel (mikroszekundum nagyságrendő), így időt lehet megtakarítani, egységnyi idő alatt több mérést tesz lehetővé (pl. hőtérképet lehet készíteni). Mozgó tárgyakon is lehetővé teszi a hőmérsékletmérést. A mérések olyan helyeken is lehetővé válnak, ahol egyébként az életveszély vagy a nehéz hozzáférés miatt eddig lehetetlen volt a mérés (nagyfeszültség, nagy mérési távolságok, magas hőmérséklet). Magas hőmérséklet mérése is lehetővé vált (egészen 3000°C-ig). Nem keletkezik interferencia. A mért tárgy nem veszít hőmérsékletéből. Pl. a csekély hővezető képességgel rendelkező anyagok, mint a műanyag, fa hımérséklete is nagy pontossággal mérhető. Nincs a mért értékek között nagy szóródás. Nem jár roncsolással, nincs mechanikai sérülésveszély a mért tárgy felületén. Lakkozott vagy puha felületek mérése is lehetséges.
Hőmérsékleti skálák
Napjainkban alapvetően három hőmérsékleti skálát használunk. Számunkra a legismertebb a Celsius-skála. Ha ezen a skálán megadnak egy hőmérséklet értéket, mindnyájan el tudjuk dönteni, hogy az hideg, meleg vagy nagyon forró. Nem tudjuk ugyanezt megtenni a főként angolszász országokban használt Fahrenheit-skála esetében. Nekünk a 100 °C forrót jelent, de nem igazán tudjuk, mit jelent a 100 °F (Fahrenheit fok). A Kelvin-skálát minden iskolás előbb-utóbb megismeri, sőt általában még az átváltás módját is ismeri.
Az egyes skálák közötti átváltás a következő:
- Celsiusról Kelvinre: T (K) = T (°C) + 273
- Kelvinről Celsiusra: T (°C) = T (K) – 273
- Celsiusról Fahrenheitre: T(°F) = 9/5T(°C) + 32
- Fahrenheitről Celsiusra: T(°C) = 5/9T(°F) – 32
Források:
- http://elte.prompt.hu/sites/default/files/tananyagok/MeteorologiaAlapismeretek/ch13s06.html
- http://tudasbazis.sulinet.hu/hu/termeszettudomanyok/fizika/fizika-10-evfolyam/homerseklet-homerok/homersekleti-skalak
- http://hvg.hu/plazs/20110805_idojaras_elorejelzes_tenyek_tevhitek
- https://qubit.hu/2018/01/31/uj-szuperszamitogeppel-kutat-az-omsz-de-miert-nem-letezik-a-tokeletes-elorejelzes-es-segithet-e-a-mesterseges-intelligencia
- https://hu.wikipedia.org/wiki/Numerikus_id%C5%91j%C3%A1r%C3%A1s-el%C5%91rejelz%C3%A9s
- http://nimbus.elte.hu/tanszek/docs/BSc/2016_2/Kovacs_Tamas_2016.pdf
- https://commons.wikimedia.org/wiki/File:2013-10-20_14_17_55_Cotton_Region_Shelter_containing_Maximum_and_Minimum_Thermometers_viewed_from_the_south.JPG
- https://manonice.com/2014/04/
- https://www.muszeroldal.hu/measurenotes/infraglobal.pdf






